
Sometimes it is specified as having exactly two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case. It cannot be used with non-right triangles. In geometry, an isosceles triangle (/ a s s l i z /) is a triangle that has two sides of equal length. The hypotenuse of a right triangle can be found using the Pythagorean Theorem, which is a theorem specific to right triangles.
#Hypotenuse of isosceles right triangle how to
How to find the hypotenuse of a right triangle How to calculate the sides of an isosceles right triangle from the hypotenuse. Since all triangles have 3 sides and 3 internal angles, it is impossible for a right triangle to have another angle that is greater than or equal to 90°, because the third angle would have to be 0° or have a negative angle measurement. This also makes sense because the internal angles of a triangle sum to 180°. Since the hypotenuse of a right triangle is the longest side of the triangle, the 90° angle opposite it is also the largest angle of the right triangle. In the Isosceles Right Triangle the adjacent sides are equal to each other, let us assume sides S and hypotenuse H. The length of a side of a triangle corresponds to the size of the angle opposite the side. The sides that form the right angle are called legs, or sometimes the adjacent or opposite side (relative to one of the angles of the triangle that is not the right angle), depending on the context. The side opposite the right angle of a right triangle is called the hypotenuse. The most popular ones are the equations: Given leg a and base b: area (1/4) × b × ( 4 × a - b ) Given h height from apex and base b or h2 height from the other two vertices and leg a: area 0.5 × h × b 0.5 × h2 × a.
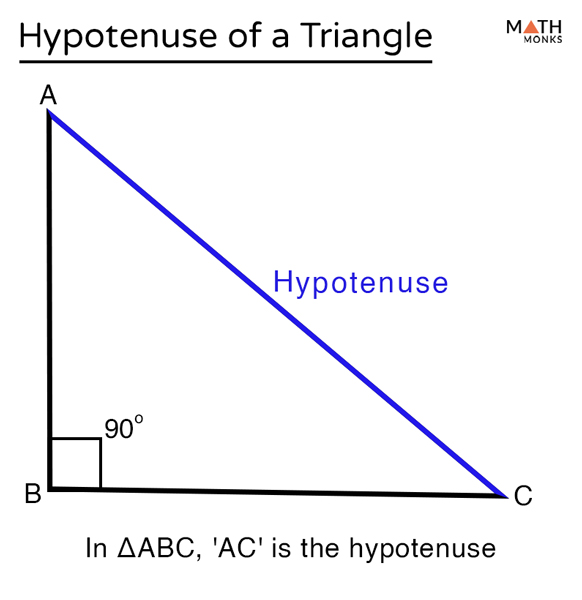

Home / geometry / triangle / hypotenuse Hypotenuse To calculate the isosceles triangle area, you can use many different formulas.


 0 kommentar(er)
0 kommentar(er)
